Workout
The Usain Bolt Guide To Blazing Speed: How The Golden Ratio Indicates Athletic Potential
Summary: We find that daVinci’s Vitruvian Man may have more to tell us than we initially gathered: it hides the potential for the optimal running angle (The Vitruvian Running Angle) and opens up questions about whether or not Usain Bolt’s near-perfect aesthetic ratios indeed are the reason that he is the fastest man alive.
************
What do the Great pyramid, a shell, and the disciple Simon Peter have in common?
The answer lies in a series of numbers named after Italian mathematician Leonardo Fibonacci of the 12th century, who introduced this remarkable sequence of numbers to Western European mathematics through his book Liber Abaci. The “Fibonacci sequence,” as it came to be known, begins with the numbers 0 and 1, followed sequentially by the sum of the previous two numbers.

The first thirteen numbers of the Fibonacci sequence are as follows:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
A peculiar feature of the Fibonacci numbers is that, when one number is divided by the previous number, the result is constantly approximately 1.618.

In fact, as the Fibonacci numbers continue in sequence, the quotient of two consecutive numbers (greater / lesser) approaches the value

This number, approximated to the value 1.618, has become known as “The Golden Ratio” because of its presence in the sequence and in our world. This golden ratio has been found in places as large as the Great pyramid and as small as our DNA. For example, the Fibonacci sequence and the golden ratio make up what is known as the golden spiral (Figure 1). This spiral can be found in shells on the beach or on the back of a snail. In this case, the Fibonacci numbers represent the growing ratio of areas within the spiral of the shell.
The Golden Ratio in the Human Body
The golden ratio has been the basis for human sculpture for centuries. Use of the golden ratio has been traced back to ancient Greece, where it was named with the Greek letter phi (ϕ) after the famous Greek sculptor Phidias. Although Leonardo da Vinci never stated in writing that he used the golden ratio in his works, it is widely believed that he was influenced by the golden ratio, as seen in his “Vitruvian Man” (Figure 2)
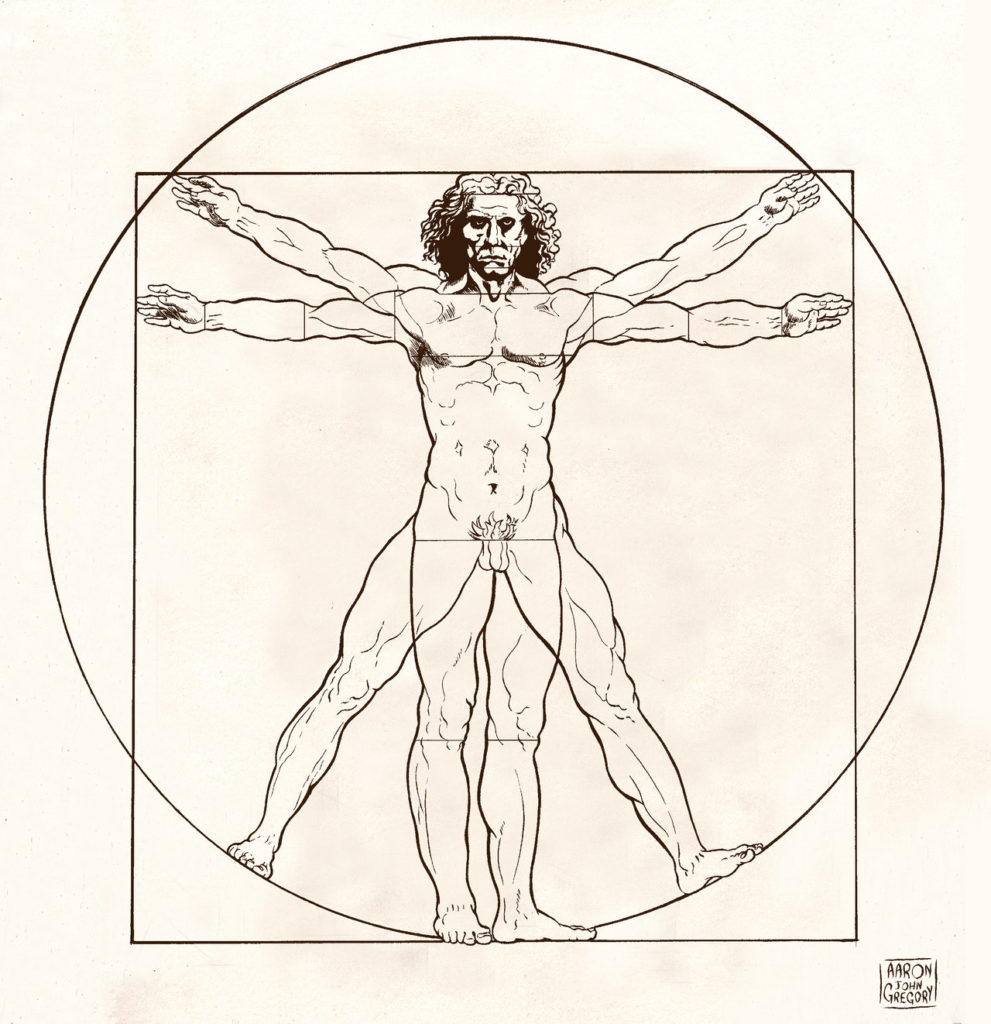
The Vitruvian Man is accompanied by notes of the famed architect Vitruvius Pollio who writes …
“For the human body is so designed by nature that the face, from the chin to the top of the forehead and the lowest roots of the hair, is a tenth part of the whole height; the open hand from the wrist to the tip of the middle finger is just the same; the head from the chin to the crown is an eighth, and with the neck and shoulder from the top of the breast to the lowest roots of the hair is a sixth; from the middle of the breast to the summit of the crown is a fourth. If we take the height of the face itself, the distance from the bottom of the chin to the underside of the nostrils is one third of it; the nose from the underside of the nostrils to a line between the eyebrows is the same; from there to the lowest roots of the hair is also a third, comprising the forehead. The length of the foot is one sixth of the height of the body; of the forearm, one fourth; and the breadth of the breast is also one fourth.”
The Vitruvian Man is the depiction of da Vinci’s “perfect man.” An interesting factor to this piece, there are instances of the golden ratio within it. The distance from the head to foot, divided by the distance from the naval to the foot is approximately 1.618. The distance between the shoulder line and the top of the head divided by the length of the head is also approximately 1.618. The golden ratio has become the basis for past and modern sculpture of the human and is believed to be the ratio for things being seen as aesthetically pleasing.
This study will go into the details and dimensions of The Vitruvian Man and the golden ratio to see what they have to tell us regarding the perfect man athletically, specifically in the area of running.
The Investigation
To begin the investigation, I began to look for instances of the possibility of the existence of the golden ratio in the running world. If the investigation seeks to analyze the ratio of perfection, then the investigation must look at the one runner who has come the closest to perfection.
That man would have to be the fastest man of all time: Usain Bolt.
It turns out, in Usain Bolt’s record-breaking 100 meter dash in 9.58 seconds, his stride rate in strides per second was approximately 4.279 strides per second and his average stride length in meters was approximately 2.439 meters per stride.
4.279/2.439 ~ 1.754
This number was close enough to the golden ratio to spark my interest. In fact, among the top 4 male sprinters of all time, Usain Bolt, Tyson Gay, Yohan Blake, and Asafa Powell (in that order), the correlation coefficient of time in the 100 meter dash to ratio of stride rate over stride length is shown in the following data analysis. (Note: only top 4 used due to lack of definitive information available)
Figure 3 (all values approximated to 3 significant figures)
| Sprinter | Usain Bolt | Tyson Gay | Yohan Blake | Asafa Powell |
| Time for 100 meters (s) | 9.58 | 9.69 | 9.69 | 9.72 |
| Stride Rate (strides/ second) | 4.28 | 4.60 | 4.45 | 4.62 |
| Stride Length (m) | 2.44 | 2.25 | 2.17 | 2.17 |
| Stride Rate / Stride Length | 1.75 | 2.04 | 2.06 | 2.13 |
(Doscher) (Why Is Usain Bolt So Fast?) (Ingle) (Phillips)

r = .9988054736
with a linear regression equation of
y = 2.71929988246x – 24.30061404
Under this regression equation, the perfect man with a ratio of stride rate to stride length of 1.618 would run a time of 9.53 seconds in the 100 meters.
1.618 = 2.71929988246x – 24.30061404
25.91861404 = 2.71929988246x
x = 9.531355758
This occurrence of the golden ratio in the races of the top sprinters of all time yields further investigation.
Is the golden ratio really the perfect running ratio, or is that just an assumption?
To answer this question, I would need a definitive model of a runner; something that could be solved using math and physics and could tell me what the perfect ratio was for stride length and stride rate
The model used in this investigation is the simple pendulum (Figure 5).
The distance the pendulum sweeps out along some arc length would substitute the stride length in the analysis and the stride rate would be calculated from the angular velocity the pendulum swings from a point of suspension. A simple pendulum swings with a massless rod, which would be thought of as the leg and the point of suspension would be where the leg ends at the top of the femur. (Figure 6)
First we must look at what happens when a simple pendulum swings about its point of suspension. To do this, the following equations are used:
ω = √(g/l)
s = l/θ
In the first equation, omega (ω) represents angular frequency in radians per second, “g” represents acceleration due to gravity, which in this investigation will be represented by the value 9.81 meters per second² and the letter “l” represents the length of the pendulum rod in meters. In the second equation the letter “s” represents arc length in meters, the letter “l” represents the length of the pendulum rod and theta (θ) represents the angle the pendulum swings forward and again backwards (see Figure 5).

When solved for “l”, the second equation becomes:
The “l” in each equation refers to the same length and each equation refers to the same pendulum, so “l” can be substituted between equations. When “l” in the first equation is substituted for “l” in the second equation, the subsequent equation becomes
ω = √(g/(s/θ)
This equation now creates a graph-able relationship between angular frequency of a pendulum and the arc length of that pendulum. Since the letter “g” represents the gravitational acceleration at 9.81 m/s², the only variable needed to graph the equation is a value for theta. In order to assume a value for theta, “The Vitruvian Man” must again be analyzed. Is Vitruvian Man telling us anything about the most efficient running form? An angular perspective of The Vitruvian Man is seen below (Figure 7).
The angle between the spread legs from naval to foot is 54 degrees. When one views the leg as the rod of the pendulum, theta is represented by the bisected angle of the 54-degree angle, making theta 27 degrees. One must note that the point of suspension in a pendulum compared to the human body would be measured at the top of the femur (see Figure 4), not the naval, but for investigative purposes, theta will be 27 degrees, as drawn in “The Vitruvian Man.”
In pendulum equations, degree values must be converted into radians. 27 degrees is equivalent to .471238898 radians. When values are substituted into their corresponding variables, the relation between angular velocity and arc length becomes
ω = √(9.81/(s/.471238898))
The graph shows the desired result of an inverse relationship between angular frequency and arc length. This is desired because, as a pendulum rod becomes longer (resulting in a larger arc length), the pendulum becomes slower (Figure 8).
Any value from the y-axis in radians per second can be converted to a linear velocity in meters per second using a simple equation.
v = ωr
The letter “v” represents the linear velocity, omega represents angular frequency, and the letter “r” represents the radius of a circle, or in our case the length of the massless rod of a pendulum in meters. Therefore, the corrected equation would be
v = ωl
The linear velocity will be the most accurate representation of a stride rate.
To calculate the linear velocity, one must have a value for “l” and a definite point on the graph in Figure 8 to substitute in for the values of “s” and omega. To find this point, the curve must be bisected so that the area under the curve to the left of that point is equal to the area under the curve to the right of that point. Since both x and y approach 0 and go to infinity, the areas under the curve are infinite in both directions. This means that, in order to split the area under the curve into two sections, the point where the coordinates of x and y are equivalent must be found. This can be done by graphing the function,
y = x
which has a slope of 1, with the function in Figure 8 and calculating the point where the two lines intersect. (Figure 9)
The point of intersection between the two functions is

Solved by

Now, with these values and the formulas, we should be able to find out what the ideal ratio between strides per second and stride length with the model of a simple pendulum. First, we must find the length of the rod of the pendulum using the formula:

With the values substituted in for our x in Figure 8 and our radian value for theta (27 degrees) we get:

With the arc length in this formula, we are using the angle of 27 degrees, which is theta in a pendulum, or the amount that the pendulum swings forward. That means the arc length obtained so far in this experiment is that of half of the pendulum, because a pendulum swings forward AND backward, as you can see in Figure 10. Therefore, in order to determine the correct arc length for the full arc traveled by a pendulum, we must multiply our half arc length (1.6658531) by two. Our new arc length is now
Now, with the value for length and a value for angular frequency, which is y on the graph, we can find the linear velocity in meters per second.

We must address the fact that a runner’s stride does not follow the pathway of arc length (Figure 10). The runner is above the ground while running and, assuming a track is entirely flat, the runner’s stride length will be a flat, straight line. Therefore, instead of using arc length for stride length, we must use the displacement of the ball of the pendulum in order to find an accurate representation of stride length.
Since theta is 27 degrees, we can take

to find half of the pendulum displacement that we can multiply by 2 to find the total pendulum displacement, so

Now that we have the linear displacement, we have an accurate representation of stride length in meters. Now we must find the accurate representation for stride rate in strides/ second. To do this we need the arc length the pendulum covers (s) and the linear velocity (v).
If we take the linear velocity (how fast the pendulum is moving in m/s) divided by the arc length (the distance covered over the period in meters), then we will be left with the value of how many arc lengths that can be covered in one second
Note: In this case, we can interchange arc length with the pendulum displacement we called stride length because the time it takes to cover each is equivalent

Results
So now we have a representative value for both stride rate and stride length using the simple pendulum

The ratio of stride rate to stride length is then

This is clearly not the ratio of ϕ. Why is this? The ϕ relationship I was looking for in the sprinting world involves countless factors of power, wind, and mental stamina. The simple pendulum does not describe power, but harmonic motion. Therefore, the model of a simple pendulum describes running in harmonic motion. This means that the less power used in the running race, the more accurate this ratio becomes. Someone may find this ratio useful in, say, an ultra marathon where power is minimal.
There are different styles of the pendulum, much more complicated, that may propose a more accurate model for a sprinter, and therefore solve the reason for the correlation coefficient seen in Figures 3 and 4. In further research, the investigation could extend to the model of the damped, driven pendulum defined under the equation below

where variables such as natural frequency, driving frequency, amplitude of the driving force, a damping coefficient and phase difference which can model external means of running such as drag (wind resistance) and opposing muscle groups.
This investigation has instead come up with some surprising results. It instead proposes a solution for the most efficient 27-degree pendulum, a pendulum that could be called “The Vitruvian Pendulum.” As mentioned before, as a pendulum rod becomes longer, it loses average linear velocity. This investigation then proposes that the most efficient Vitruvian Pendulum in terms of maximizing speed and length of rod, has the following dimensions

and therefore

with a speed to length ratio of

This is nearly ϕ, resting only approximately .04781901 off of the mark. I do believe, however, that the true ratio would turn out to be approximately 1.618 or ϕ, but due to my own personal error or oversight, have missed the mark by approximately 2.96%.
Conclusion
In conclusion, “The Vitruvian Man” may have more to tell us than we have given it credit. The use of ϕ in regards to sculpture and the golden ratio being the ratio for the most aesthetically pleasing human may only grasp at the potential of ϕ in the human body. This investigation proposes that, not only does ϕ deserve a spot in the realm of the physics of a pendulum, but also in the realm of athletics. To prove this, take a look at Figure 13, a picture of Usain Bolt, renowned as one of the greatest athletes who ever lived. A feature of the Vitruvian man and sculptures that use ϕ is that the ratio of height to the distance from naval to foot is equal to ϕ. Measure Bolt’s height and divide it by the distance from where his naval would be to his feet (see Figure 13).
By my measurements,

Usain Bolt is an almost perfect 1.619.
Being a distance runner myself, I find this investigation and the possible efficient running angle of 27 degrees very applicable to my own running career. In further research, I would like to apply the Vitruvian running angle in a data analysis and try out the 27 degree angle for the lift of my thigh in my own running to see whether or not this angle can be applied to “distance-running” levels of power.








